Verteilungen stellvertretend mit Hilfe von Mittelwerten zu charakterisieren ist gefährlich, weil verkürzend. Aber auch statistische Abweichungsmaße sind nicht besonders managementtauglich und nichts ersetzt den Blick auf die tatsächliche Verteilung der Einzelwerte.
Die Grafiken zeigen die Umsätze mit Margarine an aufeinander folgenden Tagen in drei Supermarktfilialen. In Supermarkt 1 wurde die Margarine gar nicht beworben. In Supermarkt 2 wiesen Pappaufsteller auf die Margarine hin. In Supermarkt 3 boten freundliche Damen Brotstückchen mit Margarine zum Probieren an.
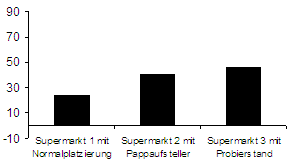
Die erste Grafik zeigt die Mittelwerte von jeweils fünf Tagesumsätzen je Supermarkt. Die Unterschiede in den Mittelwerten signalisieren eine scheinbar klare Rangfolge der Wirksamkeit. Die Darstellung ist üblich und weit verbreitet. Dennoch ist sie gefährlich und falsch. Sie suggeriert eine Sicherheit, die nicht existiert.
Nur nebenbei: Zum kaum zu widerlegenden Beweismittel würde die Darstellung, wenn sie zusätzlich mit dem Hinweis garniert wäre, es handele sich dabei um ein zum Niveau von 5% signifikantes Testresultat. Dafür sorgt die massenhysterisch anmutende Verbreitung des Missverständnisses darüber, was signifikant bedeutet, die nur vor wenigen statistischen Institutionen und kaum einem Lehrbuch Halt macht*. Davon hatten wir es kürzlich.
Der Mangel der obigen Grafik besteht darin, dass sie mehr verbirgt als sie zeigt. Nichts gibt darüber Aufschluss, wie sehr die Tageswerte um den Mittelwert streuen und ob Ausreißer das Ergebnis beeinflusst haben. Das kann zwei Ursachen haben: Der Erfinder der Darstellung ist arglos und freut sich über das Versprechen vieler Statistiksoftwarepakete, dass man sie auch ohne jeden Sachverstand anwenden kann. Oder: Der Erfinder ist sich der Schwäche der Datenlage bewusst, will aber seine Argumentation nicht den Daten, sondern die Daten seiner Argumentation anpassen. In jedem Fall ist dem Betrachter die Möglichkeit genommen mitzudenken. Reagieren Sie darauf stereotyp. Ignorieren Sie derartige Darstellungen. Anders ist ihnen auf Dauer nicht beizukommen.
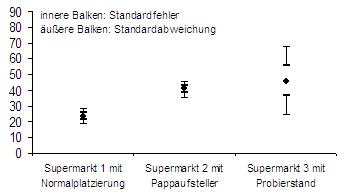
Die zweite Grafik versucht die genannten Mängel durch grafische Integration des Standardfehlers zu beheben. Damit befindet sie sich in Übereinstimmung zum Beispiel mit dem bemerkenswerten Geoffrey Loftus**. Der Standardfehler schätzt ab, wie sehr die Werte in der Grundgesamtheit streuen. Das wiederum tut er nur, wenn wir über eine große normalverteilte Stichprobe verfügen, was hier nicht der Fall ist.

Die letzte Grafik ist mein Favorit. Sie ist managementtauglich. Sie markiert für mich den Unterschied zwischen statistischen Ritualen und statistischem Denken.
*Krämer/Gigerenzer 2005, S. 6
** siehe Loftus, G.R., A picture is more worth than thousand p-values: On the irrelevance of hypothesis testing in the computer age, Behavior Research Methods, Instrumentation and Computers 25 (1993) 2, S. 250 ff, figure 3.
